
P. Kolar, M. S. Grbić, S. Hrabar, Sensors 19, 03064 (2019)
M. S. Grbić, JAP 125, 224501 (2019)
T. Cvitanić, M. Lukas, M. S. Grbić, Rev. Sci. Instrum. 90, 043903 (2019)
D. Pelc, P. Popčević, M. Požek, M. Greven, and N. Barišić, Sci. Adv. 5, eaau4538 (2019)
D. Pelc, H.-J. Grafe, G. D. Gu, and M. Požek, Phys. Rev. B 95, 054508 (2017).
R. Blinder et al. Phys. Rev. B 95, 020404(R) (2017).
D. Pelc, M. Vučković, H.-J. Grafe, S.-H. Baek, M. Požek, Nature Communications 7, 12775 (2016).
D. Pelc, M. Požek, V. Despoja and D. K. Sunko, New J. Phys. 17, 083033 (2015).
M. Došlić, D. Pelc and M. Požek, Rev. Sci. Instrum 85, 073905 (2014).
T. Cvitanić, D. Pelc, M. Požek, E. Amit, and A. Keren, Phys. Rev. B 90, 054508 (2014).
As a result of the collaboration between researchers Damjan Pelc, Miroslav Požek and Neven Barišić from the Department of Physics, with the scientists from the Institute of Physics, the Technical University of Vienna and the University of Minnesota, a paper was published in the prestigious magazine Quantum materials from the Nature journal group, in which superconductivity in dc electrical resistance is explained by a simple model of superconducting percolation.
Despite the overwhelming effort lasting several decades of many scientists around the world, understanding of the high-temperature superconductors of cuprates is still a challenge for the scientific community. It is particularly important to understand the regime of superconducting 'pre-pairing' above the macroscopic temperature of the superconducting transition - that regime gives an insight into both the normal and superconducting state. In this regard, it is a special experimental challenge to separate the superconducting response from the complex behavior of the normal state. Various experiments therefore gave contradictory conclusions about pairing above the transition temperature, which was followed by a wide range of possible theoretical explanations.
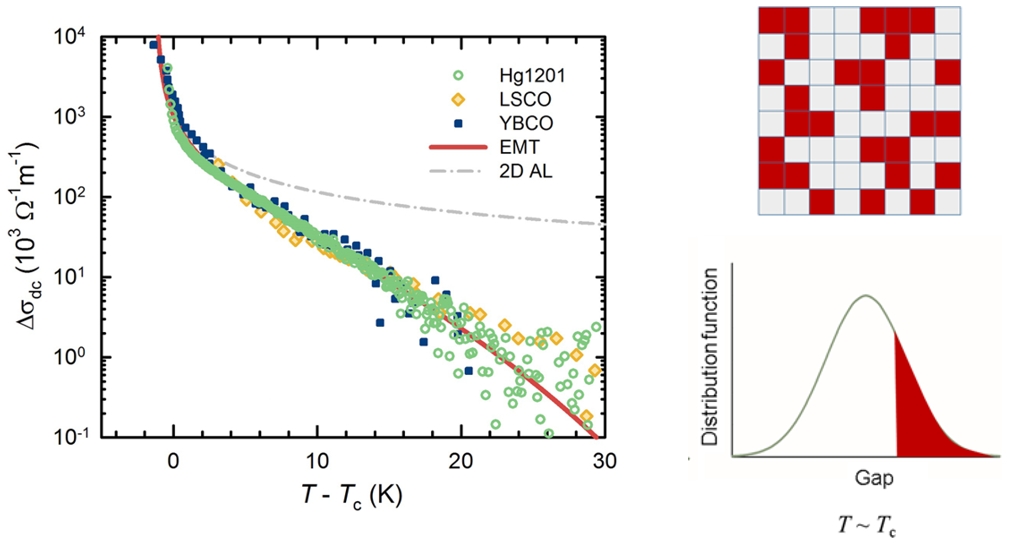
Paraconductivity obtained by subtracting the resistance of the normal Fermi liquid state from measured conductivity of several compounds from the family of cuprates. The red line represents the prediction of the model of superconducting percolations within the theory of effective media. Schematic representation of superconductive percolation model as the 2D section of the full 3D model (top row). The red parts are superconducting, while the grey parts have the resilience of the normal state. The full line represents Gaussian distribution of local transition temperatures.
In the last decade of experimental research, in which Zagreb physicists played a decisive role, it was undoubtedly established that mobile carriers in cuprates have the characteristics of conventional Fermi liquid. Although, their behavior is hidden in some parts of the phase diagram by the temperature-dependent charge (de)localization. The work presented in "Quantum materials" focuses on the underdoped area of the phase diagram of the cuprates (the so-called pseudogap area) where there is a relatively wide temperature interval with a constant number of charge carriers. In this regime, the normal resistance has a very simple square temperature dependence, according to the theory of Fermi liquid. This property was used to unambiguously separate the contribution of the normal state of electrical conductivity from the paraconducting contribution, corresponding to the appearance of superconductivity. Thus, it is shown in a clear and simple way that the traces of superconductivity can be seen only a few tens of degrees above the temperature of the superconducting transition, with a nearly exponential decrease in the paraconductive temperature dependence. It has also been shown that the dependence is universally described in cuprates, with a characteristic temperature scale that does not depend on the details of particular compounds. Finally, a simple model of superconductive percolation has been developed, within which there is a local distribution of nano-scale transition temperature, with areas with a locally elevated transition temperature. By applying effective media theory to such a system with localized superconducting areas, the temperature dependency of conduction is consistent with experiments. The good arrangement of the model and the experiment indicates that the intrinsic inhomogeneity of the superconducting state is present in the cupreates. Clear and unambiguous determination of universal superconducting percolations and another confirmation of conventional behavior of mobile charge carriers in normal conditions requires a change of established paradigms in the area of high-temperature superconductivity.