Kad kažemo kvantni magnetizam, pod tim se misli na fenomene koji su vezani za kvantne fluktuacije i osnovna stanja koja su uzrokovana kvantnim karakteristikama (ne postoji analogni klasični prikaz). Budući se radi o magnetizmu, ovakvi fenomeni nastaju kada u nekom materijal interagiraju spinovi malog iznosa; S=1/2 ili S=1.
Obično pod kvantne magnetske sisteme podrazumijevamo niskodimenzionalne sisteme (1D, 2D) jer su u njima kvantne fluktuacije najjače. Oni su pretežno izolatori, dok vodljivi kvantni sistemi organskih spojeva te teških fermiona zbog svojih specifičnosti klasificiramo u zasebne skupine.
Razmatramo li samo Heisenbergovo vezanje prvih susjeda (J) bez dodatne anizotropije, 1D sustav se ne može magnetski urediti na konačnoj temperaturi, a u slučaju da je interakcija među spinovima anitferomagnetska tada čak niti na T = 0 K. Ovo je posljedica Mermin-Wignerovog teorema koji pokazuje kako za dimenzije d<3 ne može doći do loma kontinuirane simetrije (dakle faznog prijelaza). Zbog toga se mogu ostvariti novi egzotični oblici osnovnog stanja čije istraživanje otkriva skrivene informacije o kvantnom svijetu.
Spinski lanci
Postoji razlika u vrsti osnovnog stanja za slučaj da lanac tvore jedinice spina-1/2 (S=1/2) i spina-1 (S=1). Za S=1/2, Bethe je našao da se osnovno stanje [1] sastoji od višečestičnih singleta (spin-0) bez energijskog procijepa u spektru pobuđenja. Takvo stanje, koje je zapravo superpozicija svih mogućih singletnih parova na lancu, je nazvano stanje rezonirajuće valentne veze [2]. Jake fluktuacije, tj. pobuđenja zbog zatočenosti u 1D rešetku, uzrokuju delokalizaciju singleta koji stalno fluktuiraju, raspadaju se i tvore nove parove.
.png)
Grafički prikaz rešetke (sasvim gore) i osnovnog stanja S=1/2 lanca (donje tri linije). Svaka elipsa predstavlja singletnu vezu između 2 spina. Tri točke znače da su prikazane samo neke konfiguracije fluktuirajućeg osnovnog stanja.
Međutim, za slučaj S=1 lanca fizika je sasvim drukčija [3]. Naime, dok je za S=1/2 lanac osnovno stanje tvore delokalizirani singleti (s korelacijama koje trnu ~|r|a), osnovno stanje S=1 lanca je singlet s kratkodosežnim redom gdje korelacije trnu ~e-r. U spektru pobuđenja postoji energijski procjep (Haldane procjep Δ ≈ 0.41 J) koji ukazuje da su formirani singleti lokalizirani i tvore uređeno stanje krutine valentnih veza koje se mogu prikazati na slijedeći način. Svaki spin S=1 se sastoji od dva elektrona, svaki sa S=1/2. Valentne veze se tvore između dva spina S=1/2 na dva različita čvora rešetke, i formiraju singlet. To znači da se više energije uštedi tvorbom valentnih veza između dva različita čvora rešetke, nego orijentiranjem dva spina paralelno unutar istog iona.
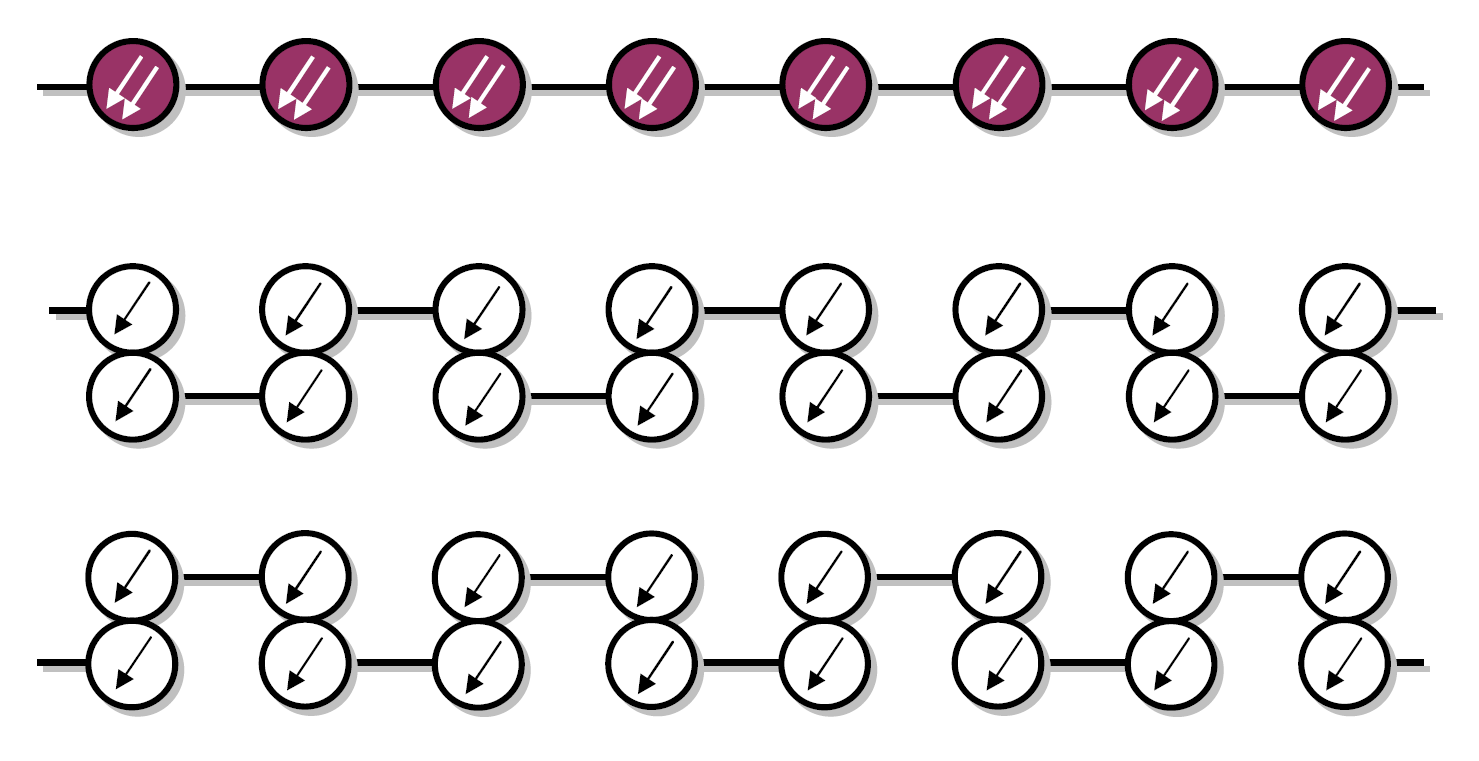
Grafički prikaz fizike S=1 lanca. (gore) 1D rešetka spinova sa S=1, (u sredini i dolje) dva degenerirana stanja krutine valentnih veza.
Opis osnovnih stanja koji je naveden ranije govori o situaciji bez vanjskog magnetskog polja. U konačnom polju osnovno stanje se može promijeniti [4]. Za S=1 1D sustave sa singletnim osnovnim stanjem, prvo pobuđeno stanje je triplet, te se porastom magnetskog polja snižava energija tripletnog stanja odnosno spinki energijski procjep se smanjuje. Ako je primijenjeno polje dovoljno veliko da se prcjep zatvori (Hc1 = Δ /g μB) osnovno stanje sustava se mijenja; križanje energijskih novoa uzrokuje formiranje nove 3D faze, koju zovemo “Bose-Einsteinova kondenzacija magnona” [5]. Vrijednost polja na kojoj singletno i tripletno stanje postaju degenerirana se naziva kvantna kritična točka a taj prijelaz induciran magn. poljem kvantni fazni prijelaz. U novo stvorenoj 3D fazi, pobuđenja su koherentna i bez procijepa, dapače potrebno je proizvoljno malo energije da bi se realizirale. Valentne veze, koje su za Hc1 bile stabilne, sada se u novoj fazi kidaju i sustav se postepeno polazirira.
Porastom magnetskog polja sustav se može provući kroz još jedan kvantni fazni prijelaz (na vrijednosti polja Hc2 = 4 J S/g μB u slučaju Haldanove faze) kada se sve valentne veze pokidaju i sustav postaje potpuno polariziran. Međutim, ako je vezanje među spinovima J prejako onda je magnetso polje Hc2 previsoko da bi se stvorilo u laboratorijskim uvjetima. Ako je J dovoljno nizak, može se opaziti promjena prirode elementarnih pobuđenja: magnoni (za Hc1 > H > Hc2) se transformiraju u spinone (Hc1 < H < Hc2). Dakle, poljem inducirana faza ima fundamentalno drukčija svojstva od polazne u H=0 T.
U realnim sustavima se vrlo često, pored jednostavnog Heisenbergovog vezanja, javljaju i različite anozotropije koje također utječu na energijsku strukturu sustava. Npr. nagnuti i anizotropni g-tenzor, Dzyaloshinkskii-Moriya interakcija među spinovima, anizotropija izoliranog iona i sl. Pod njihovim utjecajem fizikalni opis neki puta ostane neizmijenjen, a neki puta se potpuno promijeni pa je potrebno pažljivo analizirati opažanja kako bi se korektno protumačila ili naći bolji prikladniji sustav.
Za spoj DTN (skraćeno od dikloro-tetrakis tiourea-nikal(II) NiCl2-4SC(NH2)2) [6] se smatra da je modelni sustav Bose-Einstein kondenzacije magnona gdje osno-simetrična anizotropija izoliranog iona smjesti singletnu projekciju tripletnog stanja 8.9 K ispod pravih tripletnih stanja. Radi toga se lako može magnetski poljem inducirati 3D koherentna faza i proučavati svojstva nove vrste elementarnih pobuđenja. Energijski fazni dijagram ovog spoja u ovisnosti o magnetskom polju je prikazan ispod.
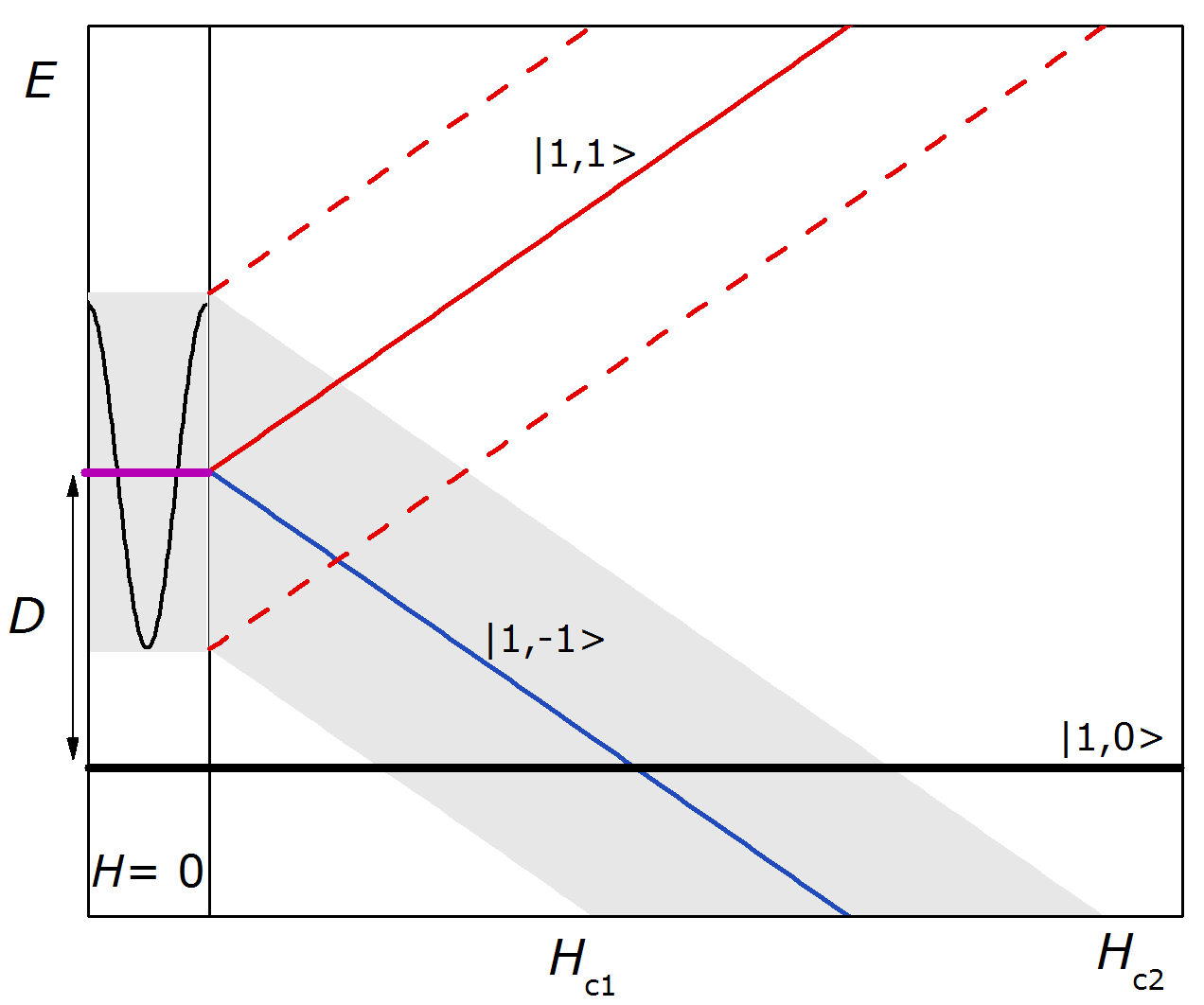
Energijski fazni dijagram spoja DTN gdje anizotropija izoliranog iona D spušta singletnu projekciju i omogućuje križanje nivoa na konačnom polju. U slučaju izoliranog spina postojalo bi samo jedno kritično polje, no interakcija među spinovima stvara energijsku vrpcu te dno i vrh vrpce kreiraju dva kritična polja: Hc1, Hc2.
A Hamiltonijan koji ga opisuje može se napisati u slijedećem obliku:
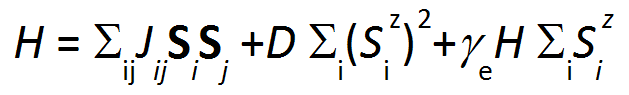
Nedavno istraživanje [7] je pokazalo kako se i na samoj kvantnoj kritičnoj točki (H = Hc1,2) ostvari novi tip kvazičestica karakterističan za 1D sustave. Taj tip kvazičestice zasada još nije predviđen, što pokazuje da je kvantna kritična tvar ovih sustava još uvijek nedovoljno istražena.
Spinski lanci su najjednostavnije građevne jedinice kvantnog magnetizma, i njihovim kombinacijama se tvore kompleksniji sustavi poput spinskih ljestvica s N-nogu, spinske tube, "spojevi telefonskih brojeva" i sl., preko kojih se dobijaju mnoge egzotične elektronske faze te nova stanja tvari.
1 Bethe, Z. Physik 71, 205 (1931).
2 P. W. Anderson, Mater. Res. Bull. 8, 153 (1973).
3 Haldane, Phys. Rev. Lett. 50, 1153 (1983).
4 Chaboussant et al., Eur. Phys. J. B 6, 167 (1998).
5 Affleck, Phys. Rev. B 43, 3215 (1991).
6 D. Reyes, A. Paduan-Filho, M. Continentino, Phys. Rev. B 77, 052405 (2008).
7 Mukhopadhyay et al., Phys. Rev. Lett. 109, 177206 (2012).

 Pristupačnost
Pristupačnost