Radom u cijelosti zamišljenom i provedenom na Fizičkom Odsjeku, prof. Denis Sunko je koristeći matematički aparat iz devetnaestog stoljeća potpuno općenito pokazao da Hilbertov prostor identičnih čestica ima finiju matematičku strukturu od beskonačnodimenzionalnog vektorskog prostora, a to je konačnodimenzionalna algebra. U praksi to znači da je konačno mnogo (anti)simetričnih funkcija dovoljno da generira sve (anti)simetrične valne funkcije, i za fermione i za bozone — kao da se reklo, umjesto beskonačno mnogo cigala ima konačno mnogo tipskih kuća. Ovaj rezultat ima široke reperkusije za kvantnu mehaniku jako koreliranih konačnih sustava. Objavljen je u časopisu Physical Review A.
Od kada ih je Dirac uveo 1926. godine, tzv. Slaterove determinante su bile jedini način da se konstruiraju valne funkcije identičnih fermiona, koje zadovoljavaju temeljni uvjet da budu antisimetrične na zamjenu čestica. Prostor mnogočestičnih stanja je vektorski (Hilbertov) prostor u kojem su vektori valne funkcije. Kao što piše u udžbenicima, Slaterove determinante su potpuna baza koja ga razapinje kao linearni prostor nad kompleksnim brojevima. S druge strane, antisimetrične valne funkcije su naprosto kompleksne funkcije, koje se očito mogu množiti bilo kakvim simetričnim funkcijama i tako dobivati nove antisimetrične funkcije. No ako su funkcije vektori, onda je to obično množenje funkcija vektorsko množenje, čime Hilbertov prostor prirodno dobiva matematičku strukturu algebre. Pokazuje se da je ova algebra konačnodimenzionalna, slično kao Liejeve algebre poznate iz teorije grupa, što znači da ima konačan broj generatora. Tehničkim jezikom, ako se kompleksni brojevi koji množe Slaterove determinante u standardnom prikazu poopće na simetrične funkcije, onda suma koja razapinje Hilbertov prostor postane konačna. Točno N!d-1 antisimetričnih funkcija razapinje cijeli Hilbertov prostor N čestica u d dimenzija, čim se dozvoli da koeficijenti u razvoju budu simetrične funkcije. Dakako, antisimetrične funkcije koje se pojavljuju kao bazni vektori u ovom razvoju — tj. generatori algebre Hilbertovog prostora — nisu proizvoljne. Konstruiran je konkretni algoritam koji ih sve pronađe kao zatvorene analitičke izraze. Prof. Sunko ih je nazvao oblici. Oblici su prava poopćenja Slaterove determinante osnovnog stanja na više od jedne prostorne dimenzije. Oni otvaraju mogućnost reformulacije niza otvorenih problema u fizici, kemiji, i istraživanjima materijala, a koji se mogu svesti na konstrukciju realističnih valnih funkcija jako koreliranih konačnih sustava.
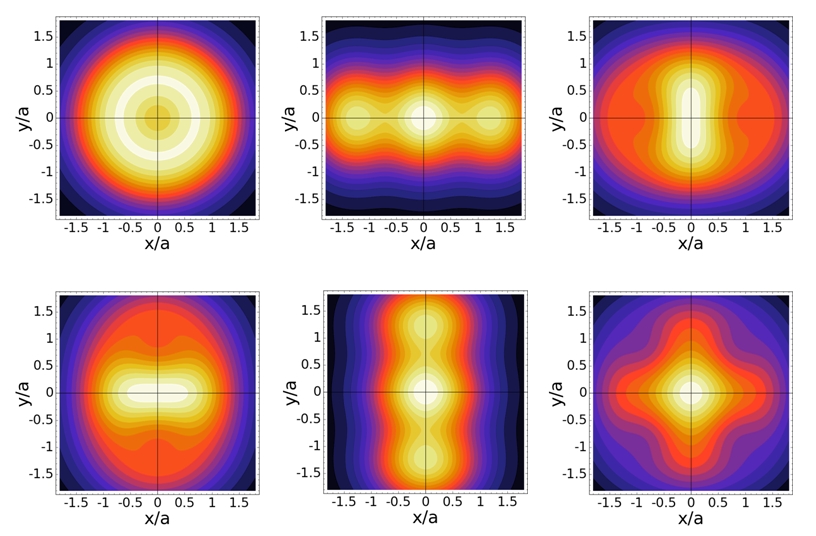
Slika prikazuje jednočestične matrice gustoće svih šest oblika tri čestice u dvije dimenzije, u potencijalu harmoničkog oscilatora. Postoje redom jedan oblik sa dva čvora, četiri oblika sa tri čvora, te jedan oblik sa četiri čvora valne funkcije. Skala je
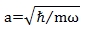
D. K. Sunko, Natural generalization of the ground-state Slater determinant to more than one dimension, Phys. Rev. A 93, 062109 (2016)
http://dx.doi.org/10.1103/PhysRevA.93.062109,
http://arxiv.org/abs/1605.06002.